Equations that relate two or more unknown variables to one another through an equal number of equations are referred to as simultaneous equations and systems of equations, respectively.

Example:

Only one pair of x and y values can be used to solve this particular set of equations.

There are an infinite number of correct (x,y) solutions for either equation when looked at independently, but when combined, there is only one. When plotted on a graph, the following condition is clear:

For this set of equations, there is but a single combination of values for x and y that will satisfy both.

Either equation, considered separately, has an infinitude of valid (x,y) solutions, but together there is only one. Plotted on a graph, this condition becomes obvious:

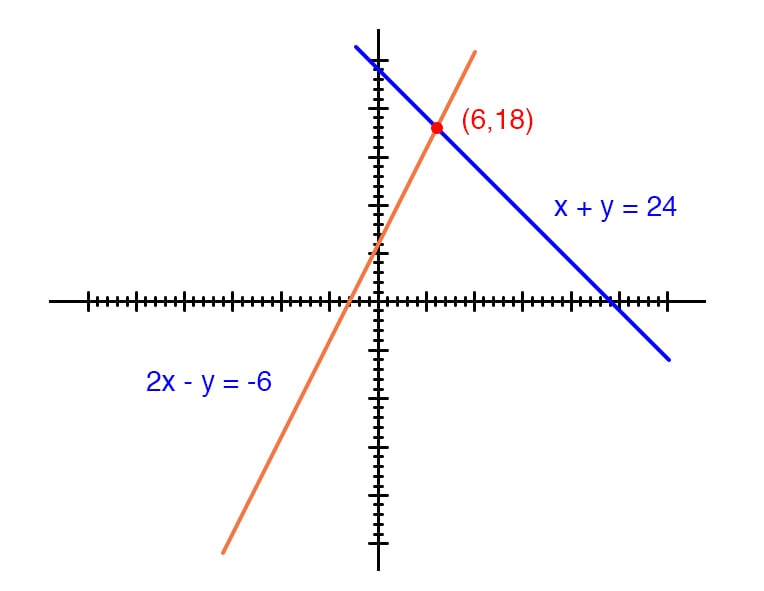
Each line is actually a continuum of points representing possible x and y solution pairs for each equation.

Each equation, separately, has an infinite number of ordered pair (x,y) solutions. There is only one point where the two linear functions x + y = 24 and 2x - y = -6 intersect (where one of their many independent solutions happen to work for both equations), and that is where x is equal to a value of 6 and y is equal to a value of 18.

Usually, though, graphing is not a very efficient way to determine the simultaneous solution set for two or more equations. It is especially impractical for systems of three or more variables.

In a three-variable system, for example, the solution would be found by the point intersection of three planes in a three-dimensional coordinate space—not an easy scenario to visualize.